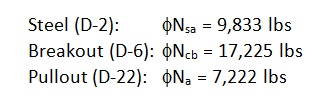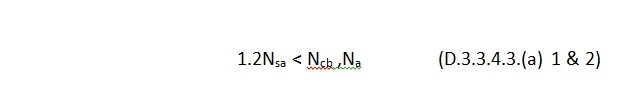We just released our updated Wood Construction Connectors catalog (C-C-2024) which features our product line that has a legacy that started in 1956. This year’s 372-page version begins with a colorful, attention-grabbing cover design and is packed inside with all the technical details that help people build safer, stronger structures. This blog is Part II of a two-part series highlighting this new catalog and the solutions inside it.
Tag: anchor
Introducing AT-3G™: Your high-strength cold-weather, fast-cure anchoring adhesive
In general, post–installed adhesive anchor design per ACI 318 Chapter 17 is relatively straightforward. In practice, however, post–installed anchorage can often become challenging because of fast–track project schedules, supply issues, ever-changing weather conditions, design conflicts/changes, or unexpected field conditions.
How to Accommodate Misplaced Shearwall Anchorage
For several years, the Simpson Strong-Tie Strong-Wall® research and development team has kicked around the idea of developing an “adapter” that would allow for field substitutions or accommodate misplaced Strong-Wall anchorage.
Questions Answered: Making the Right Anchor Choice
In this post, we follow up on our August 28 webinar, Making the Right Anchor Choice: Best Practices in Anchor Design, by answering some of the interesting questions raised by attendees.
During the webinar where we discussed the critical performance factors and code requirements you need to consider when designing with or installing adhesive or mechanical anchors. In case you weren’t able to join our discussion, you can watch the on-demand webinar and earn PDH and CEU credits here.
Continue Reading
Understanding and Meeting the ACI 318 – 11 App. D Ductility Requirements – A Design Example
If you’re one of the many engineers still confused by the ACI 318 – 11 Appendix D design provisions, this blog will help explain what’s required to achieve a ductile performing anchorage. Most building codes currently reference ACI 318 – 11 Appendix D as the required provision for designing a wide variety of anchor types that include expansion, undercut, adhesive and cast-in-place anchors in concrete base materials. This blog post will focus on section D.3.3.4.3(a) for an anchor located in a high seismic region. We’ll go over what these requirements are with a simple design example.
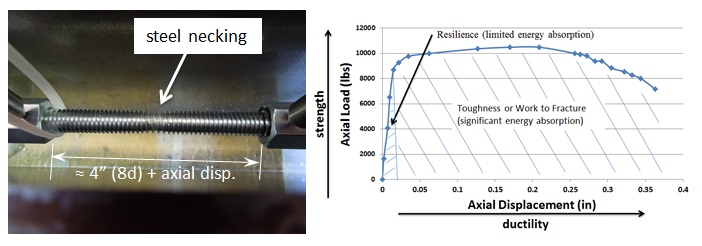
Ductility is a benefit in seismic design. A ductile anchor system is one that exhibits a meaningful degree of deformation before failure occurs. However, ductility is distinct from an equally important dimension called strength. Add strength, and a ductile steel element like the one shown in Figure 1 can now exhibit toughness. During a serious earthquake, a structural system with appreciable toughness (i.e., one that possesses both strength and ductility in sufficient degree) can be expected to absorb a tremendous amount of energy as the material plastically deforms and increases the likelihood that an outright failure won’t occur. Any visible deformations could help determine if repair is necessary.
Let’s start off with a simple example that will cover the essential requirements for achieving ductility and applies to any type of structural anchor used in concrete. We’ll arbitrarily choose a post-installed adhesive anchor. This type of anchor is very common in concrete construction and is used for making structural and nonstructural connections that include anchorage of sill plates and holdowns for shear walls, equipment, racks, architectural/mechanical/electrical components and, very frequently, rebar dowels for making section enlargements. We’ll assume the anchor is limited to resisting earthquake loading in tension only and is in seismic design category C – F. Section D.3.3.4.2 requires that if the strength-level earthquake force exceeds 20% of the total factored load, that the anchor be designed in accordance with section D.3.3.4.3 and D.3.3.4.4. We will focus on achieving the ductility option, (a), of D.3.3.4.3.
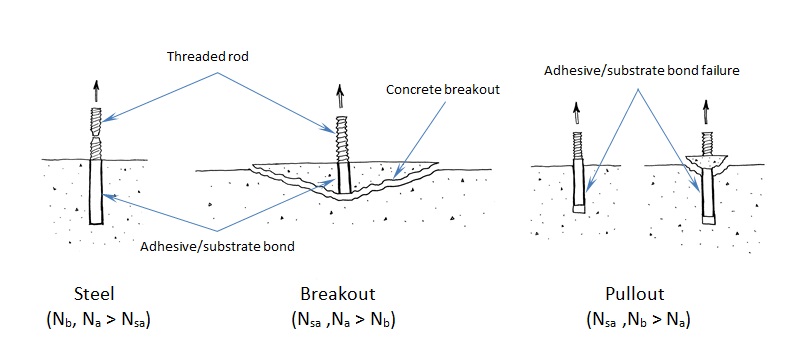
To understand anchor ductility we need to first identify the possible failure modes of an anchor. Figure 2 shows the three types of failure modes we can expect for an adhesive anchor located away from a free edge. These three failure modes generically apply to virtually any type of anchor (expansion, screw, cast-in-place or undercut). Breakout (Nb) and pullout (Na) are not considered ductile failure modes. Breakout failure (Nb) can occur very suddenly and behaves mostly linear elastic and consequently absorbs a relatively small amount of energy. After pullout failure (Na) has been initiated, the load/displacement behavior of the anchor can be unpredictable, and furthermore, no reliable mechanism exists for plastic deformation to take place. So we’re left with steel (Nsa). To achieve ductility, not only does the steel need to be made of a ductile material but the steel must govern out of the three failure modes. Additionally, the anchor system must be designed so that steel failure governs by a comfortable margin. Breakout and pullout can never control while the steel yields and plastically deforms. This is what is meant by meeting the ductility requirements of Appendix D.
Getting back to our design example, we have a single post-installed 5/8” diameter ASTM F1554 Gr. 36 threaded rod that’s embedded 12” deep, in a dry hole, in a concrete element that has a compressive strength of 2,500 psi. The concrete is 18” thick and we assume that the edge distance is large enough to be irrelevant. For this size anchor, the published characteristic bond strength is 743 psi. Anchor software calculations will produce the following information:
The governing design strength is compared to a demand or load combination that’s defined elsewhere in the code.
Here’s the question: Before proceeding with the remainder of this blog, judging by the design strength values shown above, should we consider this anchorage ductile? Your intuition might tell you that it’s not ductile. Why? Pullout clearly governs (i.e., steel does not). So it might come as a surprise to learn that this adhesive anchor actually is ductile!
To understand why, we need to look at the nominal strength (not the design strength) of the different anchor failure modes. But first let’s examine the equations used to determine the design strength values above:
The above values incorporate the notation φ (“phi”) and a mandatory 0.75 reduction factor for nonductile failure modes (Ncb ,Na) for applications located in high seismic areas (seismic design category C–F). The φ factor is defined in section D.4. However, manufacturers will list factors specific to their adhesive based on anchor testing. The mandatory 0.75 reduction comes from section D.3.3.4.4 and is meant to account for any reduction associated with concrete damage during earthquake loading. The important thing to remember is that the nominal strength provides a better representation of the relative capacity of the different failure modes. Remove these reduction factors and we get the following:
Now steel governs since it has the lowest strength. But we’re not done yet. Section D.3.3.4.3.(a).1 of Appendix D requires that the expected steel strength be used in design when checking for ductility. This is done by increasing the specified steel strength by 20%. This is to account for the fact that F1554 Gr. 36 threaded rod, for example, will probably have an ultimate tensile strength greater than the specified 58,000 psi. (Interestingly, the ultimate strength of the ½” threaded rod tested in Figure 1 is roughly 74 ksi, which is about 27% greater than 58,000 psi.) With this in mind, the next step would be to additionally meet section D.3.3.4.3.(a).2 such that the following is met:
By increasing the steel strength by 20%, the nominal strength of the nonductile failure modes (Ncb ,Na) must be at least that much greater to help ensure that a ductile anchor system can be achieved. The values to compare finally become:
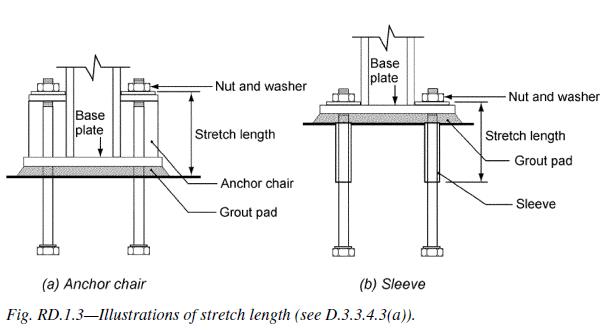
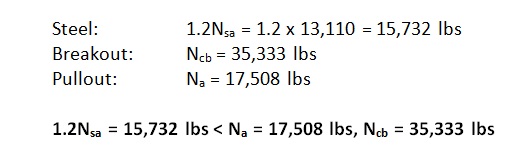 Now steel governs, but one more thing is required. As shown in Figure 3, Section D.3.3.4.3.(a).3 of Appendix D also requires that the rod be made of ductile steel and have a stretch length of at least eight times the insert diameter (8d). Appendix D defines a ductile steel element as exhibiting an elongation of at least 14% and a reduction in area of at least 30%. ASTM F1554 meets this requirement for all three grades of steel (Grade 36, 55 and 105) with the exception of Grade 55 for anchor nominal sizes greater than 2”. Research has shown that a sufficient stretch length helps ensure that an anchor can experience significant yielding and plastic deformation during tensile loading. The threaded rod shown in Figure 1 was tested using a stretch length of 4” (8d). Lastly, section D.3.3.4.3.(a).4 requires that the anchor be engineered to protect against buckling.
Now steel governs, but one more thing is required. As shown in Figure 3, Section D.3.3.4.3.(a).3 of Appendix D also requires that the rod be made of ductile steel and have a stretch length of at least eight times the insert diameter (8d). Appendix D defines a ductile steel element as exhibiting an elongation of at least 14% and a reduction in area of at least 30%. ASTM F1554 meets this requirement for all three grades of steel (Grade 36, 55 and 105) with the exception of Grade 55 for anchor nominal sizes greater than 2”. Research has shown that a sufficient stretch length helps ensure that an anchor can experience significant yielding and plastic deformation during tensile loading. The threaded rod shown in Figure 1 was tested using a stretch length of 4” (8d). Lastly, section D.3.3.4.3.(a).4 requires that the anchor be engineered to protect against buckling.
Appendix D doesn’t require that an anchor system behave ductilely. Three additional options exist for Designers in section D3.3.4.3. Option (b) allows for the design of an alternate failure mechanism that behaves ductilely. Designing a base plate (or support) that plastically hinges to exhibit ductile performance is one example. Option (c) involves a case where there’s a limit to how much load can be delivered to the anchor. Although option (c) under D.3.3.4.3 falls under the tensile loading section of Appendix D, the best example would apply to anchorage used to secure a wood sill plate or cold-formed steel track. We know from experiments that the wood crushes or the steel yields and locally buckles at a force less than the capacity of the concrete anchorage. Clearly energy is absorbed in the process. The most commonly used option is (d), which amplifies the earthquake load by Ωo. Ωo can be found in ASCE 7 – 10 for both structural and nonstructural components. The value of Ωo is typically taken to be equal to 2.5 (2.0 for storage racks) and is intended to make the anchor system behave linear elastically for the expected design-level earthquake demand.
These same options exist for shear loading cases. However, achieving system ductility through anchor steel is no longer an option for shear loading according to ACI 318 – 11, because the material probably won’t deform appreciably enough to be considered ductile.
While factors such as edge-distance and embedment-depth restrictions make achieving ductility difficult for post-installed anchors, it should come as some consolation that in many cases the Designer can achieve ductile performance for cast-in-place anchors loaded in tension through creative detailing of reinforcing steel (section D.5.2.9) to eliminate breakout as a possible failure mode. This has been explored in some detail in two previous Simpson Strong-Tie blogs titled “Anchor Reinforcement for Concrete Podium Slabs” and “Steel Strong Wall Footings Just Got a Little Slimmer.”
What are your thoughts? Visit the blog and leave a comment!
Anchor Reinforcement for Concrete Podium Slabs
How often do you get the opportunity to high five a co-worker in the office? Maybe it’s when you just worked through a complex calculation, or finally figured out that tough detail. Whatever it might be, there are times when we should raise a hand and celebrate the hard work that we do. So when we recently relaunched the Simpson Strong-Tie Strong-Rod™ Systems website, which includes a link to our new Shallow Podium Anchorage Solutions, there were a few high fives going around the office. With that in mind, we want to share the latest developments and continue our anchorage-to-concrete blog discussions that began in May 2012, continued with a March 2014 post referencing the Structure magazine article on anchor testing, and more recently one discussing our release of anchor reinforcement solutions for Steel Strong-Wall® shearwall to grade beams.
Anchor Testing for Light-Frame Construction
I started off doing a four-part series on how connectors, fasteners, concrete anchors and cold-formed steel products are tested and load rated. I realized that holdown testing and evaluation is quite a bit different than wood connector testing, so there was an additional post on holdowns. We have done several posts on concrete anchor testing (here and here), but I realize I never did a proper post about how we test and load rate concrete products per ICC-ES AC398 and AC399.
AC398 – Cast-in-place Cold-formed Steel Connectors in Concrete for Light-frame Construction and AC399 – Cast-in-place Proprietary Bolts in concrete for Light-frame Construction are two acceptance criteria related to cast-in-place concrete products.
Cold-formed steel connectors embedded in concrete are not considered in ACI 318 Appendix D, so it was necessary to create criteria for evaluating those types of connectors. Some examples of products covered by AC398 are the MASA mudsill anchor, CBSQ post base, and the STHD holdown.
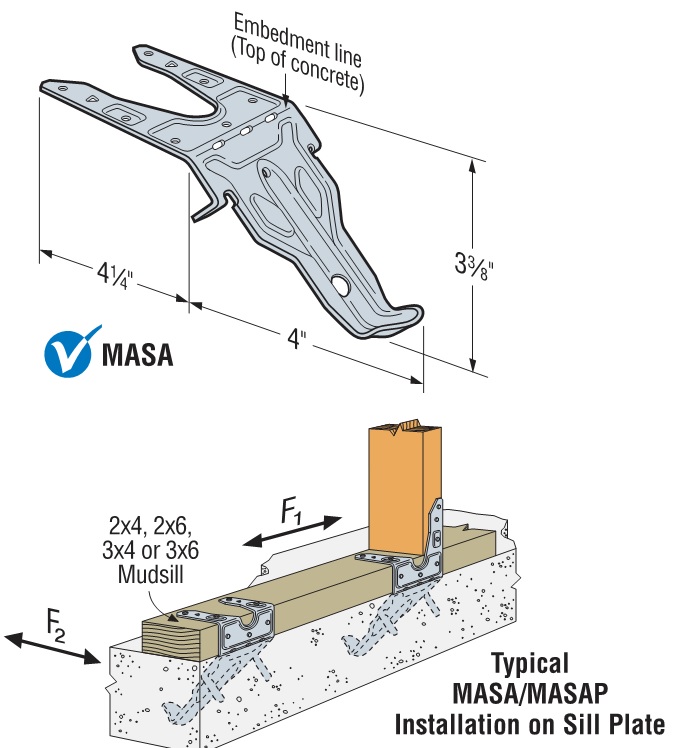
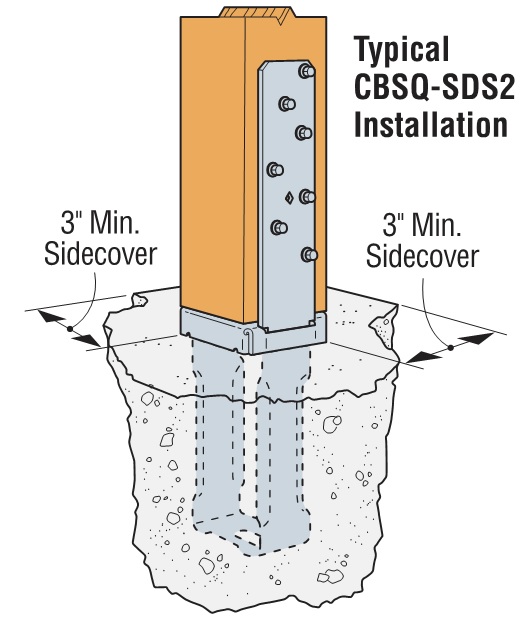
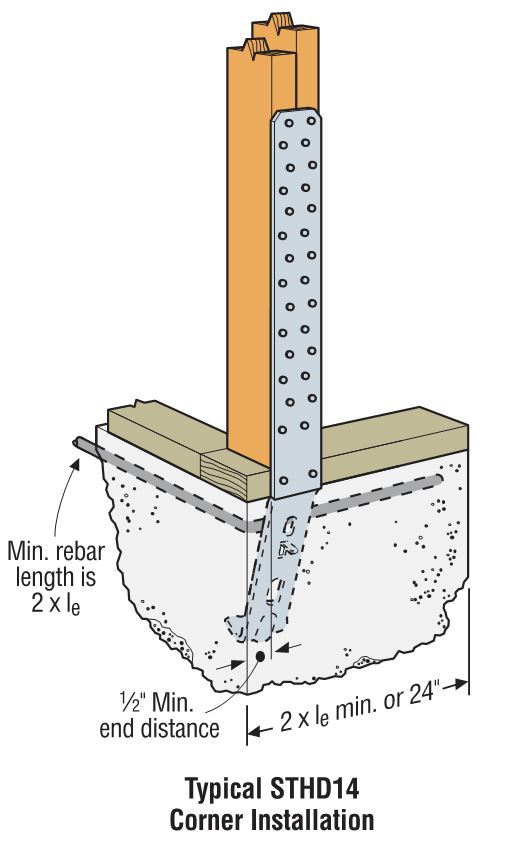
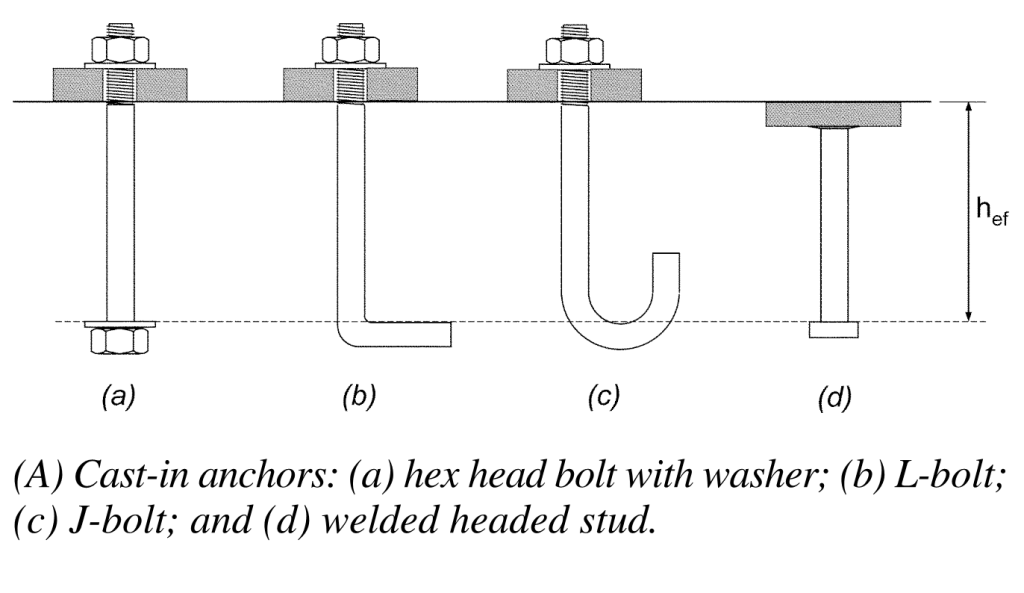
ACI 318 Appendix D addresses the design of cast-in-place anchors. However, the design methodology is limited to several standard bolt types.
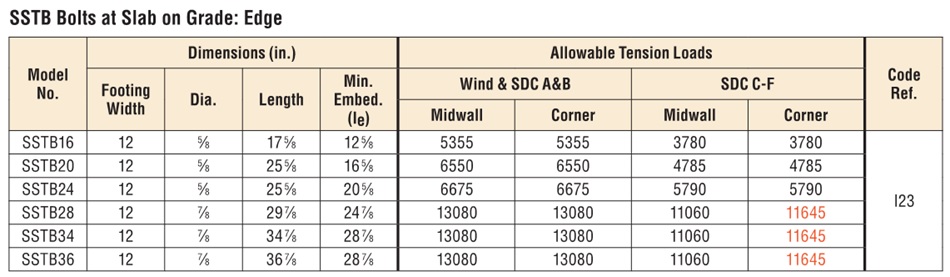
There are a number of anchor bolt products that have proprietary features that fall outside the scope of ACI 318, so AC399 fills in that gap by establishing test procedures to evaluate cast-in-place specialty anchors. Simpson Strong-Tie SB and SSTB anchor bolts are two families of anchors we have tested in accordance with AC399.
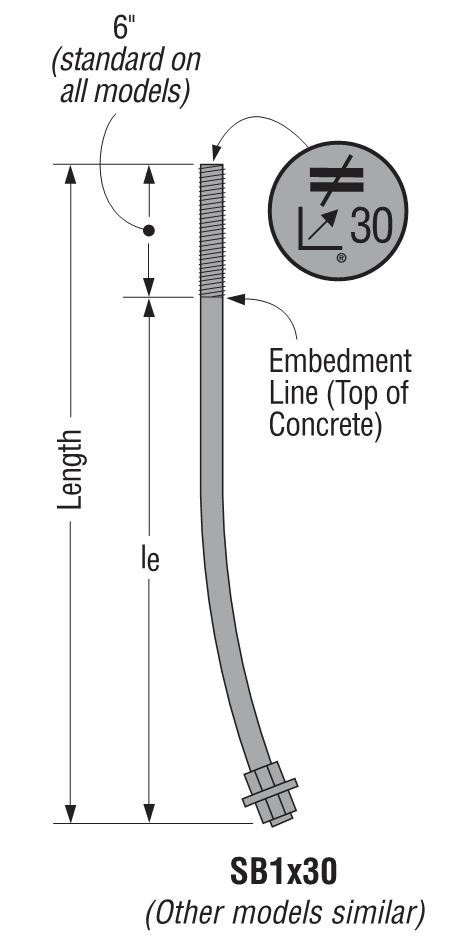
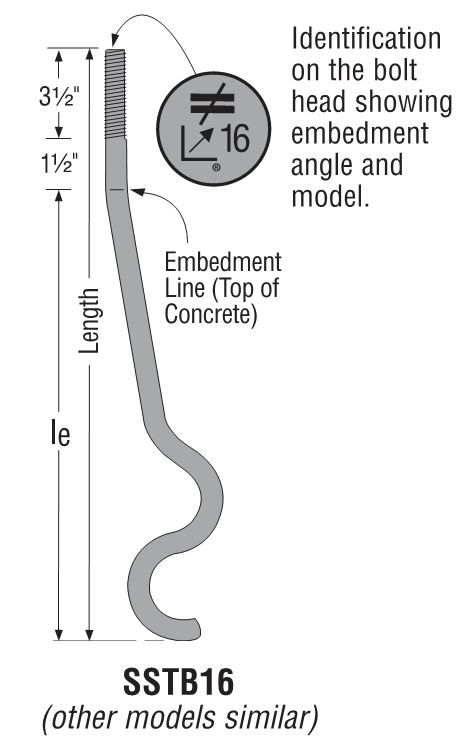
SB and SSTB anchors have a sweep geometry which increases the concrete cover at the anchored end of the bolt, allowing them to achieve higher loads with a 1¾” edge distance. The SSTB is anchored with a double bend, whereas the SB utilizes a plate washer and double nut.
AC398 (concrete connectors) and AC399 (proprietary bolts) are similar in their test and evaluation methodology. AC398 addressing both tension and shear loads, whereas AC399 is limited to tension loads. Testing requires a minimum of 5 test specimens. These are the allowable load equations for AC398 and AC399:
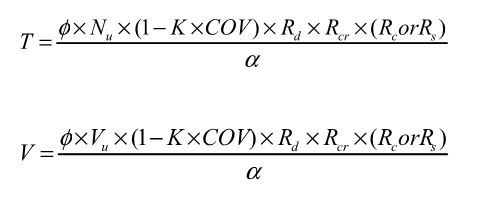
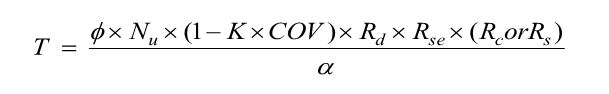
For comparison, here is the standard AC13 allowable load equation for joist hangers:
Allowable Load = Lowest Ultimate / 3
Without getting into Greek letter overload, what are these terms doing?
Nu (or Vu) is the average maximum tested load. Calculating averages is something I actually remember from statistics class. Everything else I have to look up when we do these calculations.
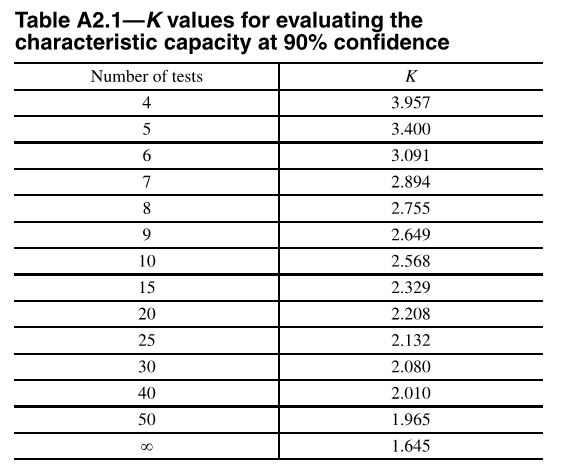
(1 – K x COV) uses K as a statistical one-sided tolerance factor used to establish the 5 percent fractile value with 90% confidence. This term is to ensure that 95% of the actual tested strengths will exceed the 5% fractile value with 90% confidence. COV is the coefficient of variation, which is a measure of how variable your test results are. For the same average ultimate load, a higher COV will result in a lower allowable load.
The K value is 3.4 for the minimum required 5 tests, and it reduces as you run more tests. As K decreases, the allowable load increases. In practice, we usually run 7 to 10 tests for each installation we are evaluating.
Rd is seismic reduction factor, 1.0 for seismic design category A or B, and 0.75 for all others. This is similar to what you would do in an Appendix D anchor calculation, where anchor capacities in higher seismic regions are reduced by 0.75.
Rs and Rc are reduction factors to account for the tested steel or concrete strength being higher than specified. There are some differences in how the two acceptance criteria apply these factors, which aren’t critical to this discussion. Φ is a strength reduction factor, which varies by failure mode and construction details. Brittle steel failure, ductile steel failure, concrete failure and the presence of supplemental reinforcement.
The α factor is used to convert LRFD values to ASD values. So α = 1.0 for LRFD and α = 1.4 for seismic and 1.6 for wind. Both criteria also allow you to calculate alpha based on a weighted average of your controlling load combinations. This has never made a lot of sense to me in practice. If you are going to work through the LRFD equations to get a different alpha value, you might as well do LRFD design.
Rse is a reduction factor for cyclic loading, which is applied to proprietary anchor bolts covered under AC399, such as the SSTB or SB anchors. A comparison of static load and cyclic load is required for qualification in Seismic Design Category C through F. Unlike the cracked reduction factor, manufacturers cannot take a default reduction if they want recognition for high seismic.
Due to the differences in AC398 and AC399 products, the load tables are a little different. AC398 products end up with 4 different loads – wind cracked, wind uncracked, seismic cracked and seismic uncracked.
AC399 products are a little simpler, having just wind and seismic values to deal with.
What are your thoughts? Let us know in the comments below.
New Simpson Strong-Tie Anchor Designer software
Remember back to the days when you used allowable stress design for designing anchorage to concrete? Once you had your design loads, selecting an anchor was quick and easy. The 1997 UBC covered the anchorage to concrete in less than two pages, so the calculation was painless. Post-installed anchors were even easier, since allowable loads were tabulated and you just needed to apply a couple of edge distance and spacing reductions.
Since the introduction of strength design provisions and the adoption of ACI 318 Appendix D, first in the 2000 IBC, designing code-compliant anchorage to concrete has become much more complex. At least once (and probably not more) armed with a pencil, calculator, and an eraser, most of us have set out to design a ‘simple’ anchorage to concrete connection using the Appendix D provisions. Several pages of calculations later (and hopefully with a solution to the problem), most of us, I imagine, came to realize that designing anchorages to concrete by hand required much more time and effort than we anticipated or could allocate time for. As a result, many of us probably created an Excel template to speed up the design process using built-in functions and some Visual Basic programming.
The question is: are you still using the template?
For me, the answer is an emphatic “NO”, mainly because the spreadsheet I created has limited capability given the complexity in adapting the design methodology to complex anchor layouts, changes to the design provisions with each new code edition, and the need to add/modify data each time a new post-installed anchor product is introduced.