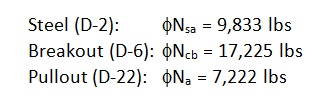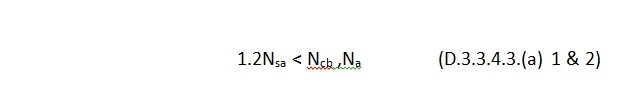Lag screws are traditionally specified for many structural loads in wood construction. However, recent innovations in engineering for self-tapping wood screws have made them an increasingly popular, labor-saving alternative to lag screws. In the following post, Aram Khachadourian, P.E., of Simpson Strong-Tie discusses the structural and economic advantages of this option.
Continue Reading
Tag: ductility
Understanding and Meeting the ACI 318 – 11 App. D Ductility Requirements – A Design Example
If you’re one of the many engineers still confused by the ACI 318 – 11 Appendix D design provisions, this blog will help explain what’s required to achieve a ductile performing anchorage. Most building codes currently reference ACI 318 – 11 Appendix D as the required provision for designing a wide variety of anchor types that include expansion, undercut, adhesive and cast-in-place anchors in concrete base materials. This blog post will focus on section D.3.3.4.3(a) for an anchor located in a high seismic region. We’ll go over what these requirements are with a simple design example.
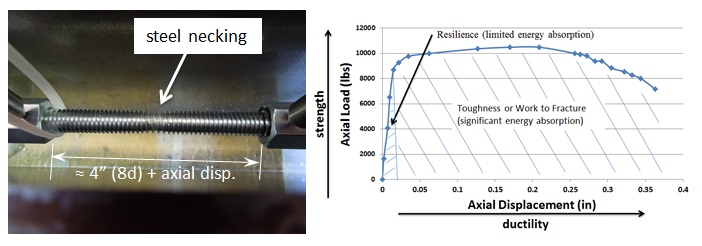
Ductility is a benefit in seismic design. A ductile anchor system is one that exhibits a meaningful degree of deformation before failure occurs. However, ductility is distinct from an equally important dimension called strength. Add strength, and a ductile steel element like the one shown in Figure 1 can now exhibit toughness. During a serious earthquake, a structural system with appreciable toughness (i.e., one that possesses both strength and ductility in sufficient degree) can be expected to absorb a tremendous amount of energy as the material plastically deforms and increases the likelihood that an outright failure won’t occur. Any visible deformations could help determine if repair is necessary.
Let’s start off with a simple example that will cover the essential requirements for achieving ductility and applies to any type of structural anchor used in concrete. We’ll arbitrarily choose a post-installed adhesive anchor. This type of anchor is very common in concrete construction and is used for making structural and nonstructural connections that include anchorage of sill plates and holdowns for shear walls, equipment, racks, architectural/mechanical/electrical components and, very frequently, rebar dowels for making section enlargements. We’ll assume the anchor is limited to resisting earthquake loading in tension only and is in seismic design category C – F. Section D.3.3.4.2 requires that if the strength-level earthquake force exceeds 20% of the total factored load, that the anchor be designed in accordance with section D.3.3.4.3 and D.3.3.4.4. We will focus on achieving the ductility option, (a), of D.3.3.4.3.
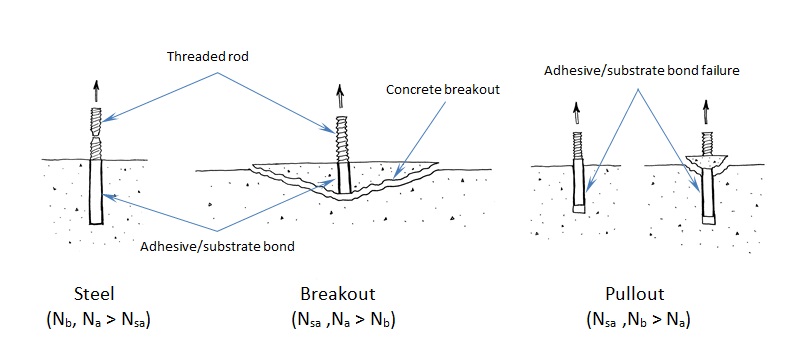
To understand anchor ductility we need to first identify the possible failure modes of an anchor. Figure 2 shows the three types of failure modes we can expect for an adhesive anchor located away from a free edge. These three failure modes generically apply to virtually any type of anchor (expansion, screw, cast-in-place or undercut). Breakout (Nb) and pullout (Na) are not considered ductile failure modes. Breakout failure (Nb) can occur very suddenly and behaves mostly linear elastic and consequently absorbs a relatively small amount of energy. After pullout failure (Na) has been initiated, the load/displacement behavior of the anchor can be unpredictable, and furthermore, no reliable mechanism exists for plastic deformation to take place. So we’re left with steel (Nsa). To achieve ductility, not only does the steel need to be made of a ductile material but the steel must govern out of the three failure modes. Additionally, the anchor system must be designed so that steel failure governs by a comfortable margin. Breakout and pullout can never control while the steel yields and plastically deforms. This is what is meant by meeting the ductility requirements of Appendix D.
Getting back to our design example, we have a single post-installed 5/8” diameter ASTM F1554 Gr. 36 threaded rod that’s embedded 12” deep, in a dry hole, in a concrete element that has a compressive strength of 2,500 psi. The concrete is 18” thick and we assume that the edge distance is large enough to be irrelevant. For this size anchor, the published characteristic bond strength is 743 psi. Anchor software calculations will produce the following information:
The governing design strength is compared to a demand or load combination that’s defined elsewhere in the code.
Here’s the question: Before proceeding with the remainder of this blog, judging by the design strength values shown above, should we consider this anchorage ductile? Your intuition might tell you that it’s not ductile. Why? Pullout clearly governs (i.e., steel does not). So it might come as a surprise to learn that this adhesive anchor actually is ductile!
To understand why, we need to look at the nominal strength (not the design strength) of the different anchor failure modes. But first let’s examine the equations used to determine the design strength values above:
The above values incorporate the notation φ (“phi”) and a mandatory 0.75 reduction factor for nonductile failure modes (Ncb ,Na) for applications located in high seismic areas (seismic design category C–F). The φ factor is defined in section D.4. However, manufacturers will list factors specific to their adhesive based on anchor testing. The mandatory 0.75 reduction comes from section D.3.3.4.4 and is meant to account for any reduction associated with concrete damage during earthquake loading. The important thing to remember is that the nominal strength provides a better representation of the relative capacity of the different failure modes. Remove these reduction factors and we get the following:
Now steel governs since it has the lowest strength. But we’re not done yet. Section D.3.3.4.3.(a).1 of Appendix D requires that the expected steel strength be used in design when checking for ductility. This is done by increasing the specified steel strength by 20%. This is to account for the fact that F1554 Gr. 36 threaded rod, for example, will probably have an ultimate tensile strength greater than the specified 58,000 psi. (Interestingly, the ultimate strength of the ½” threaded rod tested in Figure 1 is roughly 74 ksi, which is about 27% greater than 58,000 psi.) With this in mind, the next step would be to additionally meet section D.3.3.4.3.(a).2 such that the following is met:
By increasing the steel strength by 20%, the nominal strength of the nonductile failure modes (Ncb ,Na) must be at least that much greater to help ensure that a ductile anchor system can be achieved. The values to compare finally become:
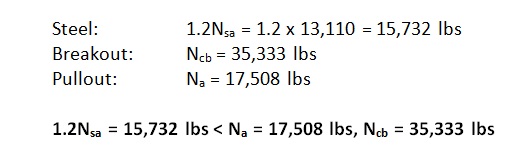 Now steel governs, but one more thing is required. As shown in Figure 3, Section D.3.3.4.3.(a).3 of Appendix D also requires that the rod be made of ductile steel and have a stretch length of at least eight times the insert diameter (8d). Appendix D defines a ductile steel element as exhibiting an elongation of at least 14% and a reduction in area of at least 30%. ASTM F1554 meets this requirement for all three grades of steel (Grade 36, 55 and 105) with the exception of Grade 55 for anchor nominal sizes greater than 2”. Research has shown that a sufficient stretch length helps ensure that an anchor can experience significant yielding and plastic deformation during tensile loading. The threaded rod shown in Figure 1 was tested using a stretch length of 4” (8d). Lastly, section D.3.3.4.3.(a).4 requires that the anchor be engineered to protect against buckling.
Now steel governs, but one more thing is required. As shown in Figure 3, Section D.3.3.4.3.(a).3 of Appendix D also requires that the rod be made of ductile steel and have a stretch length of at least eight times the insert diameter (8d). Appendix D defines a ductile steel element as exhibiting an elongation of at least 14% and a reduction in area of at least 30%. ASTM F1554 meets this requirement for all three grades of steel (Grade 36, 55 and 105) with the exception of Grade 55 for anchor nominal sizes greater than 2”. Research has shown that a sufficient stretch length helps ensure that an anchor can experience significant yielding and plastic deformation during tensile loading. The threaded rod shown in Figure 1 was tested using a stretch length of 4” (8d). Lastly, section D.3.3.4.3.(a).4 requires that the anchor be engineered to protect against buckling.
Appendix D doesn’t require that an anchor system behave ductilely. Three additional options exist for Designers in section D3.3.4.3. Option (b) allows for the design of an alternate failure mechanism that behaves ductilely. Designing a base plate (or support) that plastically hinges to exhibit ductile performance is one example. Option (c) involves a case where there’s a limit to how much load can be delivered to the anchor. Although option (c) under D.3.3.4.3 falls under the tensile loading section of Appendix D, the best example would apply to anchorage used to secure a wood sill plate or cold-formed steel track. We know from experiments that the wood crushes or the steel yields and locally buckles at a force less than the capacity of the concrete anchorage. Clearly energy is absorbed in the process. The most commonly used option is (d), which amplifies the earthquake load by Ωo. Ωo can be found in ASCE 7 – 10 for both structural and nonstructural components. The value of Ωo is typically taken to be equal to 2.5 (2.0 for storage racks) and is intended to make the anchor system behave linear elastically for the expected design-level earthquake demand.
These same options exist for shear loading cases. However, achieving system ductility through anchor steel is no longer an option for shear loading according to ACI 318 – 11, because the material probably won’t deform appreciably enough to be considered ductile.
While factors such as edge-distance and embedment-depth restrictions make achieving ductility difficult for post-installed anchors, it should come as some consolation that in many cases the Designer can achieve ductile performance for cast-in-place anchors loaded in tension through creative detailing of reinforcing steel (section D.5.2.9) to eliminate breakout as a possible failure mode. This has been explored in some detail in two previous Simpson Strong-Tie blogs titled “Anchor Reinforcement for Concrete Podium Slabs” and “Steel Strong Wall Footings Just Got a Little Slimmer.”
What are your thoughts? Visit the blog and leave a comment!
Ignore Seismic Requirements When Wind Controls?
Prior to joining Simpson Strong-Tie, my career involved the design of projects in California’s San Francisco Bay Area. When designing the primary lateral force resisting system, I would have several pages of seismic base shear calculations and, oh yeah, a one- or two-line calculation of the wind forces – just to show that seismic governed. There was no need for complete wind analysis, since the seismic design and detailing requirements were more restrictive. Of course, building components such as parapets, cladding or roof screens needed a wind design. Unfortunately, when wind appears to control, meeting the seismic requirements is not so simple.